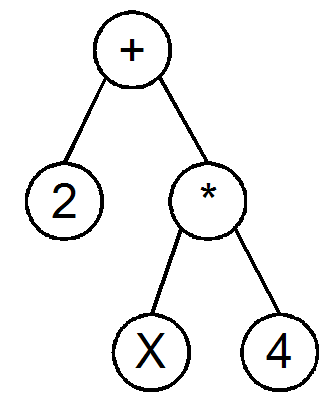Home


Modeling human expertise on a cheese ripening industrial process



Cheese Ripening

In order to make so-called "model cheeses", experimental procedures in laboratories use pasteurized milk inoculated with Kluyveromyces marxianus (Km), Geotrichum candidum (Gc), Penicillium camemberti (Pc) and Brevibacterium auriantiacum (Ba) under aseptic conditions.

During ripening, these soft-mould cheese behave like an ecosystem (a bio-reactor) extremely complex to be modeled as a whole, and where human experts operators have a decisive role. Relationships between microbiological and physicochemical changes depend on environmental conditions (e.g. temperature, relative humidity ...) and influence the quality of ripened cheeses. A ripening expert is able to estimate the current state of some of the complex reactions at a macroscopic level through its perceptions (sight, touch, smell and taste). Control decisions are then generally based on these subjective but robust expert measurements. An important information for parameter regulation is the subjective estimation of the current state of the ripening process, discretised in four phases:

Phase 1 is characterized by the surface humidity evolution of cheese (drying process). At the beginning, the surface of cheese is very wet and evolves until it presents a rather dry aspect. The cheese is white with an odor of fresh cheese.



Phase 2 begins with the apparition of a P. camemberti coat (i.e the white-coat at the surface of cheese), it is characterized by a first change of color and a "mushroom" odor development.



Phase 3 is characterized by the thickening of the creamy under-rind. P. camemberti cover all the surface of cheeses and the color is light brown.



Phase 4 is defined by strong ammonia odor perception and the dark brown aspect of the rind of cheese.



These four steps are representative of the main evolution of the cheese during ripening. The expert's knowledge is obviously not limited to these four phases, but they help to evaluate the whole dynamics of ripening and to detect drift from the standard evolution.

Evolutionary Algorithms: Cooperative co-evolution techniques

Cooperative coevolution strategies rely on a formulation of the problem to be solved as a cooperative task, where individuals collaborate or compete in order to build a solution. They mimic the ability of natural populations to build solutions via a collective process.

Instead of dealing with a coevolution process that happens between different separated populations, we use a different implementation of cooperative coevolution principles, called "Parisian approach", that uses cooperation mechanisms within a single population. It is based on a two-level representation of an optimization problem, in the sense that an individual of a Parisian population represents only a part of the solution to the problem. An aggregation of multiple individuals must be built in order to obtain a solution to the problem. In this way, the co-evolution of the whole population (or a major part of it) is favoured instead of the emergence of a single best individual, as in classical evolutionary schemes.



Genetic Programming

Genetic Programming (GP) is a specialization of genetic algorithms where each individual is a function, represented as a tree structure.

  • Nodes

    • Every tree node has an operator function: +,-,/,*, ...

    • Every terminal node has an operand: a constant or a variable

It is then easy to apply genetic operators to these trees in an evolutionary algorithm.

  • Mutations

    • Content mutation: a node is replaced with an equivalent one

    • Structure mutation: a node is replaced with a random subtree

  • Crossover

    • Swap of subtrees



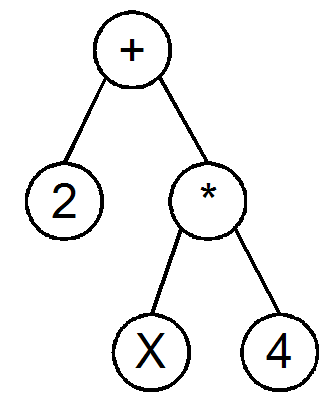
GP is used here to search for a convenient formulas that estimate the phase at time t, knowing micro-organisms proportions at the same time t, but without a priori knowledge of the phase at the time t-1. In a first classical GP approach, the phase estimator is searched as a single best "monolithic" function and then we use a cooperative scheme to split the phase estimation into four combined (and simpler) "phase detectors".

Phase estimation using a classical GP

The derivatives of four variables will be considered, namely the derivative of pH (acidity), la (lactose proportion), Km and Ba (lactic acid bacteria proportions), for the estimation of the phase. The GP will search for a phase estimator Phase(t), i.e. a function defined as follows:




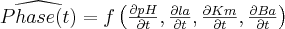
The fitness function, to be minimised, is made of a factor that measures the quality of the fitting on the learning set, plus a "parsimony" penalisation factor in order to minimize the size of the evolved structures in order to avoid bloat. It favours evolution of structures with 30 to 40 nodes. Moreover, it is divided by the number of variables involved in the evaluated tree in order to favour structures that embed all four variables of the problem.




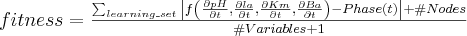
Phase estimation using a Parisian GP

Instead of searching for a phase estimator as a single monolithic function, phase estimation can actually be split into four combined (and simpler) phase detection trees. The structures searched are binary output functions (or binarised functions) that characterize one of the four phases. The population is then split into four classes such that individuals of class k are good at characterizing phase k. Finally, a global solution is made of at least one individual of each class, in order to be able to classify the sample into one of the four previous phases via a voting scheme.




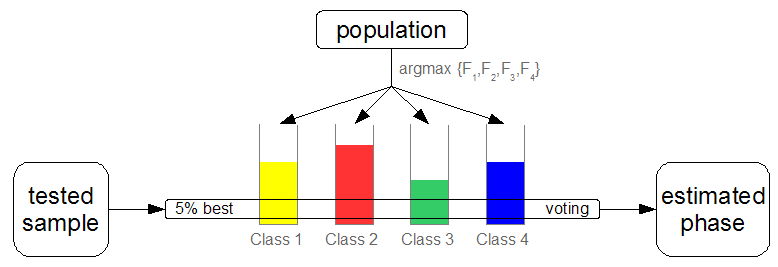
We now search for formulas I() with real outputs mapped to binary outputs, via a sign filtering: (I()>0) -> 1 and (I()<0) -> 0. The functions (except logical ones) and terminal sets, as well as the genetic operators, are the same as in the previous global approach. Using the available samples of the learning set, four values can be computed, in order to measure the capability of an individual I to characterize each phase (i.e. if I is good for representing phase k, then Fk(I) is positive for k and negative for the other values.):




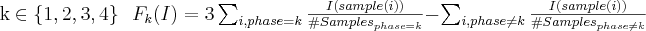
The local adjusted fitness value, to be maximised, is a combination of three factors:




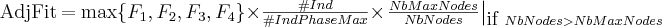
The first factor is aimed at characterising if individual I is able to distinguish one of the four phases, the second factor tends to balance the individuals between the four phases (#IndPhaseMax is the number of individuals representing the phase corresponding to the argmax of the first factor and #Ind is the total number of different individuals in the population) and the third factor is a parsimony factor in order to avoid large structures.

At each generation, the population is shared in four classes corresponding to the phase each individual characterises the best. The 5% best of each class are used via a voting scheme to decide the phase of each tested sample. The global fitness measures the proportion of correctly classified samples on the learning set and is distributed as a multiplicative bonus on the individuals who participated in the vote

Experimental analysis

Available data have been collected from 16 experiments during 40 days each, yielding 575 valid measurements. It is to be noticed that collecting these experimental data was a long and difficult process, so these resulting data sets are often uncertain or even erroneous. For example, a complete cheese ripening process last 40 days, and some tests are destructive, i.e a sample cheese is consumed in the analysis. Other measurements require to grow bacterias in Petri dishes and then to count the number of colonies, which takes a lot of time.

Experiments show that both GP outperform other available methods (multilinear regression and Bayesian network) in terms of recognition rates. Additionally the analysis of a typical Parisian GP run shows that much simpler structures are evolved: The average size of evolved structures is around 30 nodes for the classical GP approach and between 10 and 15 for the Parisian GP.

It has also to be noted that co-evolution is balanced between the four phases, even if the third phase is the most difficult to characterize (this is in accordance with human experts' judgement, for which this phase is also the most ambiguous to characterize)


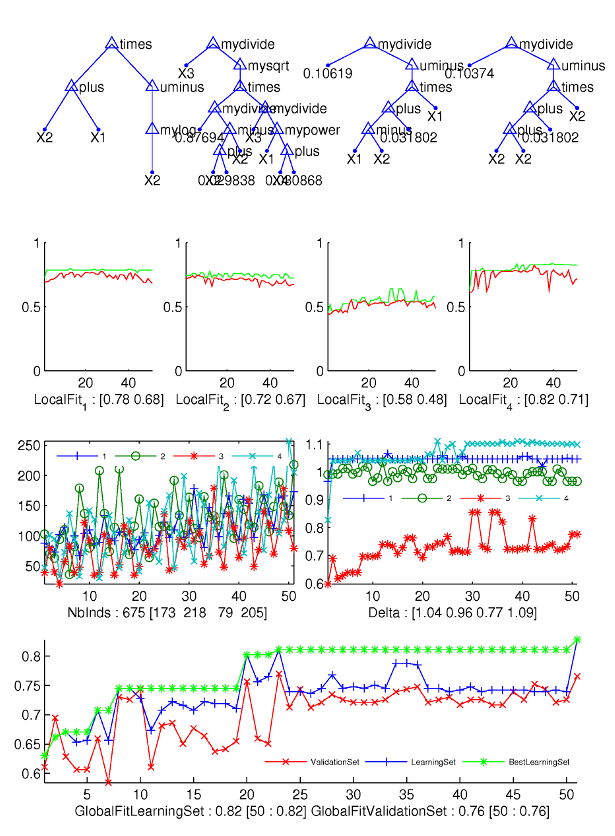
A typical run of the Parisian GP:



Variable population size strategies in a Parisian GP

Despite of local elitism and bonus mechanisms, the global fitness is not a monotonically increasing function. In particular, it often happens that a generation notably improves the global fitness, while the generations that follow are not able to keep it. To avoid this undesirable effect, a variable sized population Parisian GP strategy is experimented, using adaptive deflating and inflating schemes for the population size.

The idea is to group individuals with the same characteristics into "clusters" and remove the most useless ones at the end of every generation while periodically adding "fresh blood" to the population (i.e. new random individuals) if a stagnation criterion is fulfilled.


Individuals having the same rawfitness are grouped into clusters. Then, inside each cluster, individuals are sorted according to their number of nodes. The first and best one is the one with the smallest number of nodes.

Useless individuals elimination allows to decrease the population size: An individual is considered as useless if it belongs to a big cluster and has a large number of nodes. The elimination rule depends on two parameters (tokeep and toremove): if a cluster has less than tokeep individuals, they are all kept, and if it has more, only the last toremove, having the largest number of nodes, are removed.







In order to avoid stagnation due to over-specialisation of the best individuals, we propose to periodically add "fresh blood" to the population (i.e. new random individuals) if a stagnation criterion is fulfilled. The corresponding algorithm uses one parameter denoted toinsert, typically set to a lower value than tokeep

In this way, if a cluster of the old population is empty or has not enough elements according to a stricter rule than during the elimination process, it gets new elements.

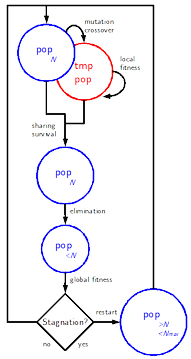
The full inflating-deflating scheme is made of the following steps:

  • mutations and crossover yield a temporary population tmppop

  • local fitness is computed on the temporary population: localfitness(tmppop)

  • adjusted fitness is computed via sharing: sharing(pop+tmppop)

  • selection of the N best individuals: pop=survival(pop+tmppop)

  • elimination of the useless individuals: pop=elimination(pop)

  • global fitness computation of the global fitness of the population: globalfitness(pop)

  • partial restart if a stagnation criterion is met: pop=restart(pop)

With the deflating+inflating scheme, there are improvements of the global fitness all along the generations. The final recognition rate on the learning set is better than with the two other schemes. As far as the size of the population is concerned, one can observe the cycles of deflations and partial restart. The population is still quite balanced between the four classes, and the number of unique individuals is also quite stable.




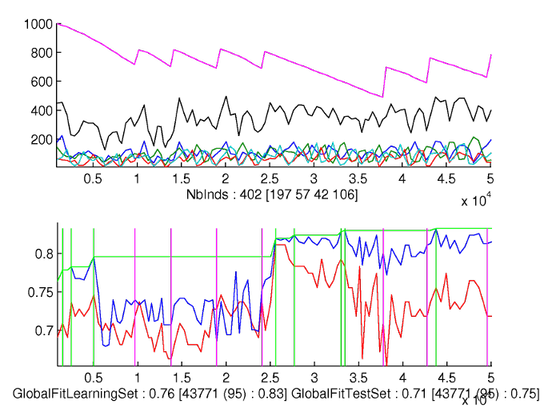
This first attempt to manage varying population sizes within a Parisian GP scheme show the effectiveness of the population deflation-inflation scheme in terms of computational gain and quality of results on a real problem. The deflating scheme allows to obtain the same result as the fixed-size population strategy, but using less fitness evaluations. The deflating-inflating strategy improves the quality of results for the same number of fitness evaluations as the fixed-size strategy.

More generally, the deflation-inflation scheme has two major characteristics: a clusterisation-based redundancy pruning and a selective inflation, which tries to maintain limited-size clusters with low complexity individuals. These two concurrent mechanisms tends to better maintain low complexity individuals as well as genetic diversity. These characteristics may actually be transposed to classical GP or EAs, in particular to limit GP-bloat effects.

Home